图像变换

本章图像变换指光谱变换，是利用单波段或多波段中的相关信息对像素值进行的数学变换。
在图像处理中，所谓图像变换可以理解为达到图像处理某种目的而使用的数学方法，通过这种数学变换，图像处理起来较变换前更加方便和简单。由于这种变换方法是针对图像函数而言，所以称之为图像变换。图像变换可以在图像校正前进行，也可以在图像校正后进行。

图像变换的目的

简化图像处理
构建图像特征
图像压缩
增强图像信息
两个过程：正变换和逆变换

傅里叶变换

傅里叶变换是一种线性积分变换，将满足一定条件的函数使用三角函数（正弦或余弦）或其积分的线性组合来表示，其研究与应用己有100多年历史，但仅在1965年快速傅里叶变换（FFT）算法出现后才得到了大规模的应用。数字图像处理中所用的傅里叶变换均属于FFT。
傅里叶变换分为连续傅里叶变换和离散傅里叶变换，在数字图像处理中使用的是二维离散傅里叶变换。

$Y=f(x,y)$空间域：研究对象是空间坐标的函数
$Y=f(\omega)$频率域：研究对象是频率的函数

设 $x(t)$ 为 $(-\infty,+\infty)$ 上的连续函数，在一定条件下，有如下关系:
$$
\begin{array}{l}
X(f)=\int_{-\infty}^{+\infty} x(t) \mathrm{e}^{-j 2 \pi f t} \mathrm{d} t \
x(t)=\int_{-\infty}^{+\infty} X(f) \mathrm{e}^{j 2 \pi f t} \mathrm{d} f
\end{array}
$$

式一称为傅里叶变换，式二称为傅里叶逆变换。由式一和式二可知，$X（ f ）$和$x（t）$一一对应。我们称无$X（ f ）$为$x（t）$的连续频谱，通常简称为频谱。根据式（6-1)，可以山信号$x（t）$求出相应的频谱$X（f）$ ，这个过程称为频谱分析。在图像处理中，该过程称为傅里叶正变换。

通过传感器接收到的信号$x(t)$，一般都包含两个成分：①有效信号$s(t)$，它是我们所需要的，使我们能够了解研究对象的性质；②干扰信号$n(t)$，它不是我们需要的，对研究对象的性质起破坏作用。这两种成分合在一起就是实际得到的信号：
$$
x(t)=s(t)+n(t)
$$
信号处理的一个主要目的就是削弱干扰$n(t)$，保持或增强信号$s(t)$。

横向和纵向频率相加
$$
\mathrm{F}(\mathrm{u}, \mathrm{v})=\frac{1}{\mathrm{NM}} \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} \mathrm{f}(\mathrm{x}, \mathrm{y}) \mathrm{e}^{-\mathrm{j} 2 \pi(\mathrm{ux} / \mathrm{N}+\mathrm{vy} / \mathrm{M})}
$$
$$
\mathrm{F}=\frac{1}{\mathrm{NM}} \sum_{x=0}^{N-1} \sum_{y=0}^{M-1} \mathrm{f}(\mathrm{x}, \mathrm{y})
$$

图像中灰度变化剧烈程度平面空间上的梯度

傅里叶变换具有的对称性，频率域图像往往以**图像中心为坐标原点，左上一右下、右上一左下对称。图像中心为原始图像的平均亮度值，频率为0；从图像中心向外，频率增高，图像中的高亮度表明该处频率特征明显。此外，频率域图像中明显的频率变化方向与原始图像中的地物分布方向相垂直。**也就是说，如果原始图像中有多种水平分布的地物，那么频率域图像中在垂直方向的频率变化比较明显。如果原始图像中地物左下一右上分布，那么频率域图像中在左上一右下方向频率变化比较明显，反之亦然。频率域图像中暗的越多，表明原图像中面越多；亮点或亮条带越多，则表明原图像中边比较多。

变换后的图像更强调频率的分布
一高频成分：梯度高，空间变化快
一低频成分：背景，空间变化慢
FFT变换耗用的内存是图像大小的8倍左右
数据要求：偶数行，偶数列
空间域和频率域同一位置所代表含义不同
频率域任意像素位置的值都是由空间域整体计算所得

波段运算

波段运算对每个像素进行计算，因此，参加运算的图像其空间坐标和大小必须完全相同。参与运算的数据，可以是单个波段，多个图像波段、常数（至少一个是波段）或文件。如果是两个图像文件间的运算，图像文件中的波段数目和顺序必须相同。

同一图像的不同波段
同一区域的不同图像波段相加

加法运算 $b3=b1+b2$
差值运算 $b3=b1-b2$
乘法运算 $b3=b1xb2$
比值运算 $b3=b1/b2$

目的

• 加
  减少图像的随机噪音，增强图像信息。
• 减
  消除影响中不希望的附加模式如阴影、周期性噪声等，提取变化信息。
• 乘
  利用卷积来实现图像的平滑，锐化，消除图像中的噪音、图像掩膜。
• 除
  扩大不同地物的光谱差异，区分在单波段中容易发生的混淆地物，消除或减弱地形阴影、云影影响和植被干扰以及显示隐伏构造等。

差值运算

• 利用不同地物之间光谱的特征
• 有利于突出目标与背景反差小的信息(红外波段-红波段，突出植被)

比值运算

两个波段的比值
目的：

• 减轻地形的干扰(如果阴坡的坡度大于太阳高度角，则难于处理)
• 扩展地物，特别是植被间的光谱差异
• 抑制大气的影响
• 减少了数据之间的相关性

植被指数

比值植被指数 $R V I=\frac{I R}{R}$
归一化植被指数 $N D V I=\frac{I R-R}{I R+R}$
差值植被指数 $D V I=I R-R$
正交植被指数 $P V I=1.6225(I R)-2.2978(R)+11.0656$

逻辑运算

$(b1 gt b2): If b1 > b2 then 1 else 0$
$(b 1 gt b 2)^{\star} b 1+b 2 / 2$
$(b 4 g t b 3)x(b 4-b 3)$

其他运算

$float(b1)$
$b1/b2$
$float(b1)/float(b2)$
$b1/max(b1)$
$float(b1)/float(max(b1))$
$byte(b1)$

K-L变换

Hotelling（霍特林变换）
主成分PCA变换

• 目的
  减少图像波段之间的相关性，去除多余的信息，减少图像的数据量
• 方法
  统计学中的正交变换方法

主成分分析(prmcipal component analysis，PCA)是统计分析中常用的方法，其求解过程与K-L变换有所不同：K-L变换是基于图像协方差矩阵进行的计算，而PCA不限于协方差矩阵（也可以是相关矩阵等）。遥感图像处理软件中的PCA有选项供选择，默认时使用协方差矩阵进行计算，结果就是K-L变换。也就是说，PCA中包括了K-L变换。K-L变换的目的是去除图像中的噪声和干扰，进行数据压缩和信息增强。

设图像数据X(n,m,k)(n行,m列,k个波段)，对于任一位置，可以用K个指标来描述
我们希望能用K1个指标来描述，其中K1<K，而且信息没有太大的失真。在统计学中，该方法称为降维

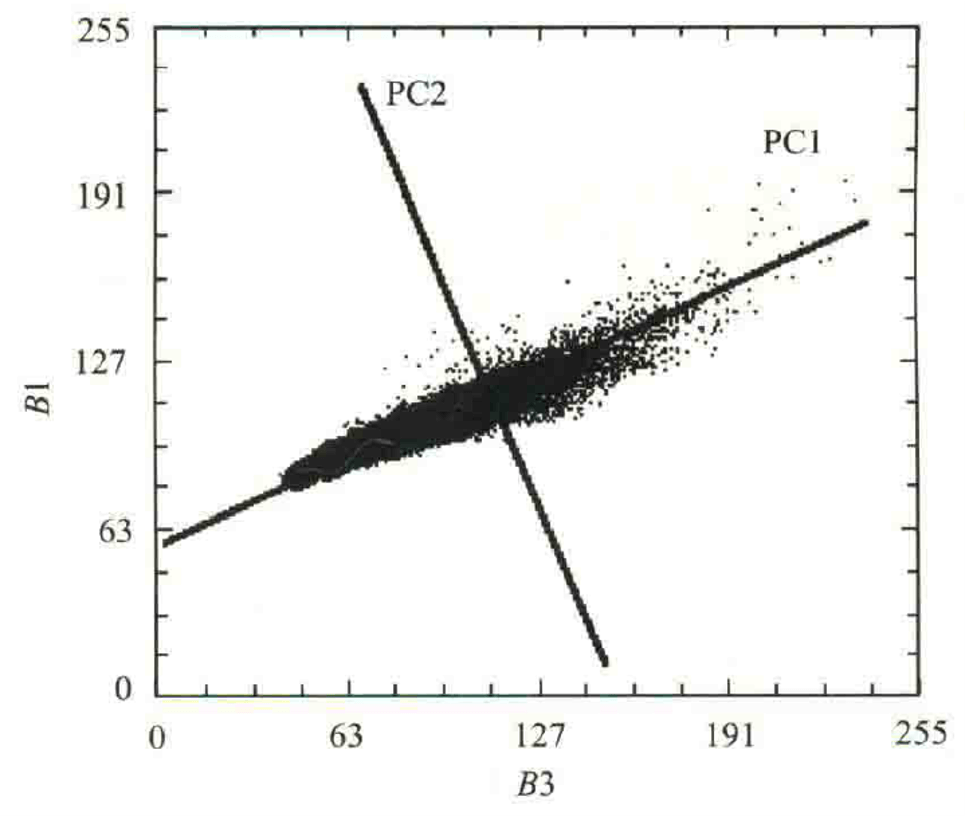
主成分
$P=f(xi),Xi$：第i个自变量
对于遥感图像：
$$
P=f(Bi)
$$
例如TM的第一主成分:
$$
P1=a+a1b1+a2b2+a3b3+..+a7b7
$$
(a0,a1,..a7可以大于0，也可以小于0)

KCL变换和PCA变换

• 协方差矩阵：载荷矩阵为K-L变换结果（K-L变换，用于降维
• 相关系数矩阵：载荷矩阵为狭义PCA变换结果（狭义主成分分析，用于分析

PCA与因子分析

• PCA是因子分析中求解的因子的一种方法
• 因子分析包括更多的因子求解方法

变换的性质和特点

• 正交性
  变换后，各个成分之间不存在相关性

• 变换前后方差总和不变。
  变换后方差在各个成分之间进行重新分配。如果波段之间具有很强的相关性，那么，第一主成分将具有最大的代表性（具有最大的方差比例）

• 在主成分中，各个波段的系数反映了该波段对该主成分的影响程度

• 适用于高通滤波，线性增强，密度分割等

• 基本性质

  1. 总方差的不变性
  2. 正交性
  3. 前面的p个主成分包含总方差的大部分

• 变换后保留的主成分个数的衡量指标：$V=\sum_{i=1}^{p} \lambda_{i} / \sum_{i=1}^{n} \lambda_{i}$

缨帽变换

• 经验性的多波段图像的正交变换方法
• 又叫K-T变换
• 1976年，R.J.Kauth, G.S. Thomas

为了看到缨帽的最大剖面，做线性变换
$$
U=R_{1} \cdot X+r
$$
初期变换后有：
$$
U=\left(u_{1}, u_{2}, u_{3}, u_{4}\right)^{T}
$$
X为像素的光谱向量，U为变换后新空间的像素向量，其各分量表示变换后每一通道的像素亮度值，r为避免出现负值而加的常数，一般为0，R1为一变换矩阵，行与行之间相互正交，
K-T变换在实际应用时舍掉第4个分量，只取前3个分量。U1为亮度分量，U2和U3分别反映了植物的绿度和黄度，绿度说明了植物的生物量状况，黄度说明了植物的枯萎程度。

1984年， Crist，Cicone 提出了LANDSAT 4的TM图像的K-T变换公式
$$
U=R_{2} \cdot X+r
$$
X为TM的第1，2，3，4，5，7波段图像上的灰度值组成的光谱向量
U为变换后的光谱向量，包含6个新分量
目前软件、文章中使用最多的公式

K-T变换的前3个分量的实际物理意义

• 亮度:实际是TM的6个波段的加权和，反映了总体的反射值。
• 绿度:反映了近红外与可见光部分的差值，绿色生物量的特征。
• 湿度:反映了可见光和近红外（1-4波段）与较长的红外（第5，7波段）的差值，定义为湿度的根据是第5，7两个波段对土壤湿度和植物湿度最为敏感 。

K-T变换系数汇总

• 基于MSS的DN
• 基于L4TM的DN应用广泛；反射率
• 基于L5TM的DN、反射率
• 基于L7ETM+的反射率、DN

研究MSS遥感数据产生

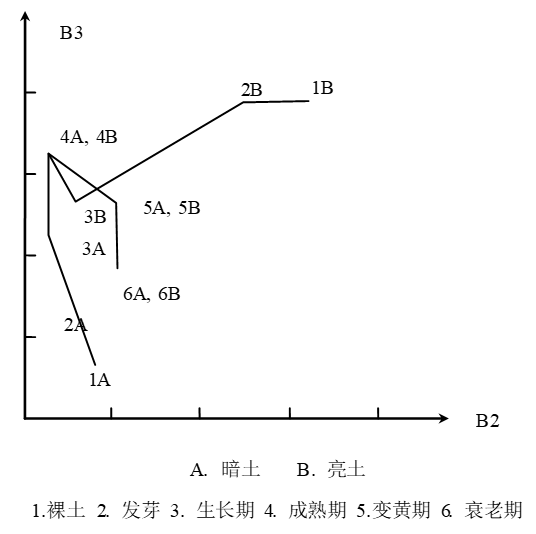
首先，在第2波段和第3波段组成的子空间中（如（a）所示），当植物还没发芽时，各种裸露的土壤，由深色土壤逐步过渡到浅色土壤形成一条土壤线，由土壤线上各点作起始点都能勾绘出一条农作物的生长线（图中只画出了从最深和最浅的两点开始的生长线）。1处为裸土，只反映了土壤本身的光谱特性；2处为农作物破土出露，随着农作物生长，植被覆盖面也越来越大。与此同时，由于太阳光从偏东方向入射时，使得植物阴影的影响增加，像素的光谱值是作物、阴影和土壤的综合反映，这时，对于深色土壤，阴影影响不大，所以随着作物覆盖的增加，波段3上绿色植物近红外的反射急剧增大，生长线上升；对于浅色土壤，阴影影响较大，减少了原像素中高亮度的土壤光谱的影响，所以尽管绿色作物近红外光谱反射随着覆盖的增加而增加。但综合效应并没有使这条生长线升高。直到农作物成熟期的到来（即图中标号4处），绿色覆盖达到高峰。几乎不能得到土壤的信息，也没有明显的阴影区，两条生长线才合为一点，不再有区别。可以推理，其他土壤类型的生长线也必定到达这里，
汇合后一起继续发展，当农作物成熟变黄时，生长线向回折返，离开绿色生物量点，经过标号5处后光谱特性继续变化，直到农作物衰老死亡到达标号6处。待农作物全部收获完毕，地面状态恢复，从标号6处应该各自回到土壤线上的起点位置（深色土壤1A处或浅色土壤1B等等）。

推广到一般农作物的生长过程

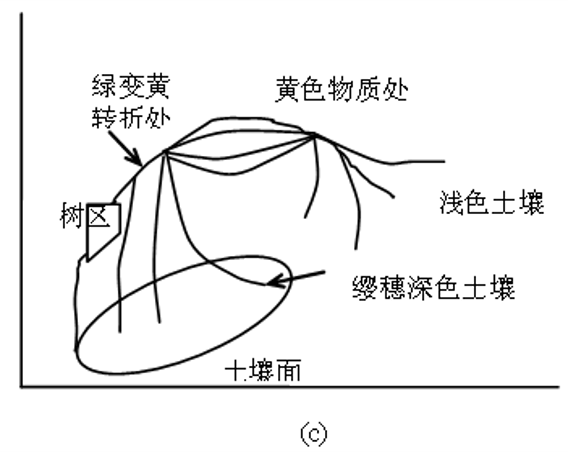
这里土壤反射光谱形成土壤面，**农作物则从土壤面开始生长，几乎沿着垂直于土壤面的方向沿不同路线，形成绿色植物区，到交汇处开始折返，并会聚于黄色植物区，最后又应回到它原来出发的土集面起点处。**这样的三维立体形态看起来很像一顶戴着缨穗的帽子，衰老处像一束缨子，土壤面就像帽口，由这一外观的想象形成了另一个名字“缨帽变换”。

K-T变换应用

• 特点
  效果优于K-L和（5，4，3）彩色合成
  具有明确的物理意义（绿度、湿度等）
  在K-T变换后的图像中，水体信息和植被信息得到了明显的
• 增强
  K-T变换的逆变换可用来去除TM图像中的霾（haze）
• 局限性
  如果区域的土壤，植被和湿度的分布不平衡或差异小，变换的效果不好
  只能用于MSS数据和LANDSAT4、5的TM图像、LANDSAT7的ETM图像
• 区别
  K-T变换与K-L变换不同。前者对于图像中各个组分的分离，特别是土壤和植被的分离，更具有优越性，变换系数与具体的图像无关。K-L变换中各成分的系数与具体的图像有关：图像不同，系数不同。

彩色变换

H——hue 色调
I——Intensity 强度
S——Saturation 饱和度
RGB 从物理的角度出发描述颜色
HSI 从人眼的主观感觉出发描述颜色

R>B≤G或0≤F<1
正变换
$$
\begin{array}{l}
I=(R+G+B) / 3 \
H=\frac{(G-B)}{3(I-B)} \
S=1-B / I
\end{array}
$$
逆变换
$$
\begin{array}{l}
R=I(1+2 S-3 S H) \
G=I(1-S+3 S H) \
B=I(1-S)
\end{array}
$$

G>R≤B或1≤H<2
正变换
$$
\begin{array}{l}
I=(R+G+B) / 3 \
H=\frac{(B-R)}{3(I-R)+1} \
S=1-R / I
\end{array}
$$
逆变换
$$
\begin{aligned}
R &=I(1-S) \
G &=I(1+5 S-3 S H) \
B &=I(1-4 S+3 S H)
\end{aligned}
$$

B>G≤R或2≤H<3
正变换
$$
\begin{array}{l}
I=(R+G+B) / 3 \
H=\frac{(R-G)}{3(I-G)+2} \
S=1-G / I
\end{array}
$$
逆变换
$$
\begin{array}{l}
R=I(1-7 S+3 S H) \
G=I(1-S) \
B=I(1+8 S-3 S H)
\end{array}
$$

• 通过对强度I成分的处理进行图像的增强（去云、去雾）
• 多源数据的综合显示
• 其它应用
  1. 对色调进行分段扩展，以突出某一色调或加大某一范围内的色调之间的差异。
  2. 色调不变，将亮度和饱和度置为常数，以突出地物色调在空间上的分布。
  3. 将强度置为常数，色调和饱和度不变，可以减少地形起伏的影响，突出阴影部分的地物信息。

数字图像融合

图像融合是数据融合的一部分，是各种图像变换方法的综合应用，用来增强图像的空间分辨率或光谱分辨率。

在遥感图像中，图像融合指多传感器、多时段、多分辨率图像的融合，主要内容包括：①定性和定量数据的融合；②相同分辨率的不同平台测量数据的融合；③不同分辨率不同平台测量数据的融合。

综合不同传感器图像的优点，增强图像信息量或分辨力的图像处理方法。

融合的两个图像之间的空间分辨率不要超过5倍。

1. K-L变换融合
   先对图像进行K-L正变换，然后用高空间分辨率图像替换第一主成分，再进行图像逆变换即得到融合后的图像。优点是可以对多个波段进行融合增强，空间信息较好，缺点是被替换掉的第一主成分包含最大的信息，使得全色波段的信息被最大化，弱化了色彩信息。
2. 彩色变换融合
   选择三个波段进行RGB合成，然后进行彩色变换为HSI，用高空间分辨率图像替换 I 成分，再进行彩色逆变换即得到融合后的图像。缺点是只能对三个波段进行融合增强，且容易导致色彩失真。在融合前可先对全色波段和 I 图像进行直方图匹配，对色调H和饱和度S进行必要的拉伸增强。

注意：进行融合的输入图像空间上必须精确配准